- FUJIMURA Hidenori, HAMAMOTO Ko, MIZUNO Takayuki, OCHIAI Osamu, SATO Aki-Hiro, TAKEUCHI Wataru, “Validation of SDG Indicator 11.3.1 (Ratio of land consumption rate to population growth rate),” Report of the Meeting for Promotion of the Use of Big Data No,03 (June 2022)
- FUJIMURA Hidenori, HAMAMOTO Ko, ISHIDA Chu, KAWAKITA Shiro, MIZUNO Takayuki, SATO Aki-Hiro, TAKEUCHI Wataru, “Validation of SDG Indicator 15.4.2 (Mountain Green Cover Index),” Report of the Meeting for Promotion of the Use of Big Data No,01 (June 2021)
- Aki-Hiro Sato, Shoki Nishimura, Tsuyoshi Namiki, Naoki Makita, Hiroe Tsubaki, World Grid Square Data Reference Framework and its Potential Applications, Conference: 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), pp. 398-409 (2018), DOI: 10.1109/COMPSAC.2018.00062
- Aki-Hiro Sato, Shoki Nishimura, Naoki Makita, Tsuyoshi Namiki, and Hiroe Tsubaki, World Grid Square Statistics and their application to data analytics, Joint UNECE/UN-GGIM Workshop on Integrating Geospatial and Statistical Standards, Stockholm, Sweden, 6-8 November 2017
- Aki-Hiro Sato, Shoki Nishimura, Hiroe Tsubaki, “World grid square codes: Definition and an example of world grid square data”, 2017 IEEE International Conference on Big Data (Big Data), pp. 4238–4247 (2017), DOI: 10.1109/BigData.2017.8258450
In 1960, the Statistics Bureau of Japan began to study the definition of grid squares for computing spatial statistics from a horizontal perspective across Japanese government ministries and departments. In the 1970s, they proposed grid square codes computed based on geographical position (latitude and longitude). In 1973, “Standard Grid Square and Grid Square Code Used for the Statistics” was made as to the Announcement No. 143 of the Administrative Management Agency (AMA) that hierarchically defines grid squares covering the entire land of Japan, and this definition was adopted by the Japanese Industrial Standards Committee in 1974. Adopting this definition, Japanese government ministries and departments and Japanese firms in industrial sectors have created grid square statistics for the purposes of planning, assessment, and evaluation in policy-making.
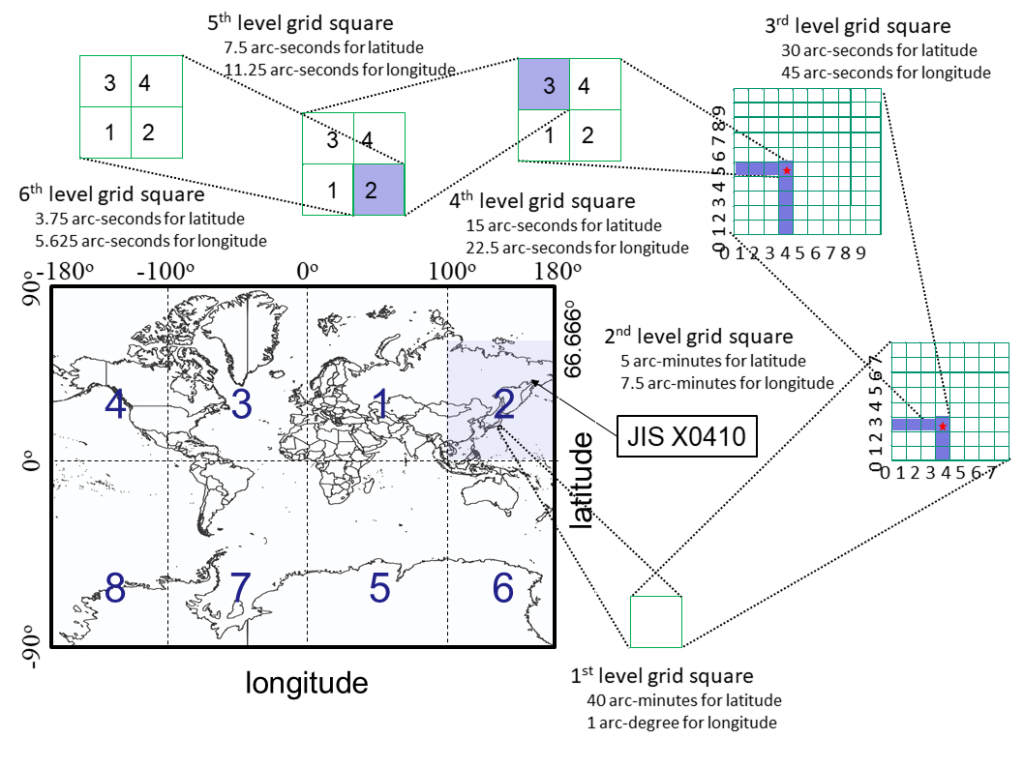
Here, we explain how to construct a World Grid Square coding system by adding the upper two numeric digits to Japanese grid square codes (JIS X0410:2002). The World Grid Square system has higher compatibility with the Japanese grid square coding system (JIS X0410). TheWorld Grid Square coding system includes six levels of spatial resolution and enables the identification of each grid square by its unique numeric digits (world grid square code) and JIS X0410. No grid square overlaps with any other grid square, and each square’s code can be calculated from geographic information (latitude and longitude).
Consider eight areas separated by latitude and longitude as shown in Figure 1.
- 1. Variable $x=0$ if latitude is positive. Otherwise $x=1$.
- 2. Varialbe $y=0$ if longitude is positive. Otherwise $y=1$.
- 3. Variable $z=0$ for $|\mbox{longitude}|<100^{\circ}$. Otherwise $z=1$.
Finally, we define 0’th level grid square code as
\begin{equation}
o=2^2 x + 2 y + z + 1.
\end{equation}
From 0’th level grid square code $o$, we obtain $x$, $y$ and $z$, respectively, as
\begin{eqnarray}
z &=& (o – 1) \mbox{ mod } 2, \\
y &=& ((o – z – 1) \div 2) \mbox{ mod } 2, \\
x &=& (o – 2 \times y – z – 1) \div 4,
\end{eqnarray}
Therefore, when we have a geographic position $(\mbox{latitude},\mbox{longitude})$, then the 1st-level grid square code can be described as
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0u & (p < 10, u < 10) \\
o0p0u & (10 \leq p < 100, u < 10) \\
op0u & (p \geq 100, u < 10) \\
o00pu & (p < 10, u \geq 10) \\
o0pu & (10 \leq p < 100, u \geq 10) \\
opu & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
the 2nd level grid square code can be described as
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqv & (p < 10, u < 10) \\
o0p0uqv & (10 \leq p < 100, u < 10) \\
op0uqv & (p \geq 100, u < 10) \\
o00puqv & (p < 10, u \geq 10) \\
o0puqv & (10 \leq p < 100, u \geq 10) \\
opuqv & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
the 3rd level grid square code can be described as
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrw & (p < 10, u < 10) \\
o0p0uqvrw & (10 \leq p < 100, u < 10) \\
op0uqvrw & (p \geq 100, u < 10) \\
o00puqvrw & (p < 10, u \geq 10) \\
o0puqvrw & (10 \leq p < 100, u \geq 10) \\
opuqvrw & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
the 4th level grid square code is computed from
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2 & (p < 10, u < 10) \\
o0p0uqvrws_2 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2 & (p \geq 100, u < 10) \\
o00puqvrws_2 & (p < 10, u \geq 10) \\
o0puqvrws_2 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
the 5th level grid square code is computed from
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
and
the 6th level grid square code is computed from
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4s_8 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4s_8 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4s_8 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4s_8 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4s_8 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4s_8 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
where integers calculated from latitude and longitude as follows:
\begin{equation}
\left\{
\begin{array}{l}
p: = \lfloor (1-2x)\mbox{latitude} \times 60 \div 40 \rfloor \quad (\mbox{$p$ is two or three digits}),
\\
a := \bigl\{(1-2x)\mbox{latitude} \times 60 \div 40 – p\bigr\} \times 40, \\
q := \lfloor a \div 5 \rfloor \quad (\mbox{$q$ is one digit}),
\\
b := (a \div 5 – q) \times 5,
\\
r := \lfloor b \times 60 \div 30 \rfloor \quad (\mbox{$r$ is one digit}),
\\
c := (b \times 60 \div 30 – r) \times 30,
\\
s_{2u} := \lfloor c/15 \rfloor \quad (\mbox{$s_{2u}$ is one digit}),
\\
d := (c/15-s_{2u}) \times 15,
\\
s_{4u} := \lfloor d/7.5 \rfloor \quad (\mbox{$s_{4u}$ is one digit}),
\\
e := (d/7.5-s_{4u}) \times 7.5,
\\
s_{8u} := \lfloor e/3.75 \rfloor \quad (\mbox{$s_{8u}$ is one digit}),
\\
u := \lfloor (1-2y)\mbox{longitude} – 100z \rfloor \quad (\mbox{$u$ is one or two digits}),
\\
f := (1-2y)\mbox{longitude} – 100z – u,
\\
v := \lfloor f \times 60 \div 7.5 \rfloor \quad (\mbox{$v$ is one digit}),
\\
g := (f \times 60 \div 7.5 – v) \times 7.5,
\\
w := \lfloor g \times 60 \div 45 \rfloor \quad (\mbox{$w$ is one digit}),
\\
h := (g \times 60 \div 45 – w) \times 45,
\\
s_{2l} := \lfloor h/22.5 \rfloor \quad (\mbox{$s_{2l}$ is one digit}),
\\
i := (h/22.5-s_{2l}) \times 22.5,
\\
s_{4l} := \lfloor i/11.25 \rfloor \quad (\mbox{$s_{4l}$ is one digit}),
\\
j := (i/11.25-s_{4l}) \times 11.25,
\\
s_{8l} := \lfloor j/5.625 \rfloor \quad (\mbox{$s_{8l}$ is one digit}),
\\
s_2 := s_{2u} \times 2+s_{2l}+1 \quad (\mbox{$s_{2}$ is one digit}),
\\
s_4 := s_{4u} \times 2+s_{4l}+1 \quad (\mbox{$s_{4}$ is one digit}),
\\
s_8 := s_{8u} \times 2+s_{8l}+1 \quad (\mbox{$s_{8}$ is one digit})
\end{array}
\right..
\end{equation}
Contrarily, if we have the 1st-level grid square code $opu$ ($o$(1 digit), $p$(3 digits), and $u$(2 digits)), then $\mbox{latitude}$ and $\mbox{longitude}$ at its northwestern corner can be computed as
\begin{eqnarray}
\mbox{latitude} &=& (1-2x) \bigl\{(p-x+1) \times 40 \ \div 60 \bigr\}, \\
\mbox{longitude} &=& (1-2y) (100 \times z + u+y ).
\end{eqnarray}
If we have the 2nd-level grid square code $opuqv$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), and $v$(1 digit)), then latitude and longitude at its northwestern corner can be computed as
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl\{p \times 40 \ \div 60 \\
&+& (q-x+1) \times 5 \div 60 \bigr\}, \\
\label{eq:expression2:latitude-mesh-2}
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u \\
\nonumber
&+& (v+y) \times 7.5 \div 60 \bigr).
\label{eq:expression2:longitude-mesh-2}
\end{eqnarray}
When the 3rd-level grid square code is given as $opuqvrw$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), and $w$(1 digit)), latitude and longitude at its northwestern corner can be computed as
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
&+& (r-x+1) \times 30 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-3}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
&+& (w+y) \times 45 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-3}
\end{eqnarray}
When the 4th-level grid square code is given as $opuqvrws_2$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), and $s_2$(1digit)), latitude and longitude at its northwestern corner can be computed as
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
&+& (\lfloor (s_2-1)/2 \rfloor + x-1) \times 15 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-4}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-4}
\end{eqnarray}
When the 5th-level grid square code is given as $opuqvrws_2s_4$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), and $s_4$(1 digit)), latitude and longitude at its northwestern corner can be computed as
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& (\lfloor (s_2-1)/2 \rfloor + x-1) \times 15 \div 3600 \\
&+& (\lfloor (s_4-1)/2 \rfloor + x-1) \times 7.5 \div 3600\bigr), \\
\label{eq:expression2:latitude-mesh-5}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-5}
\end{eqnarray}
When the 6th-level grid square code is given as $opuqvrws_2s_4s_8$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), $s_4$(1 digit), and $s_8$(1 digit)), latitude and longitude at its northwestern corner can be computed as
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& (\lfloor (s_2-1)/2 \rfloor + x-1) \times 15 \div 3600 \\
\nonumber
&+& (\lfloor (s_4-1)/2 \rfloor + x-1) \times 7.5 \div 3600 \\
&+& (\lfloor (s_8-1)/2 \rfloor + x-1) \times 3.75 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-6}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
\nonumber
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \\
&+& (((s_8-1) \mbox{ mod } 2) – y) \times 5.625 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-6}
\end{eqnarray}
| $x$: latitude | $y$: longitude | $z$: range of longitude | $x|y|z$ | decimal expression |
|---|---|---|---|---|
| $0$: $\mbox{latitude} \geq 0^{\circ}$ | $0$: $\mbox{longitude} \geq 0^{\circ}$ | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $0|0|0$ | $1$ |
| $0$: $\mbox{latitude} \geq 0^{\circ}$ | $0$: $\mbox{longitude} \geq 0^{\circ}$ | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $0|0|1$ | $2$ |
| $0$: $\mbox{latitude} \geq 0^{\circ}$ | $1$: $\mbox{longitude} < 0^{\circ}$ | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $0|1|0$ | $3$ |
| $0$: $\mbox{latitude} \geq 0^{\circ}$ | $1$: $\mbox{longitude} < 0^{\circ}$ | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $0|1|1$ | $4$ |
| $1$: $\mbox{latitude} < 0^{\circ}$ | $0$: $\mbox{longitude} \geq 0^{\circ}$ | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $1|0|0$ | $5$ |
| $1$: $\mbox{latitude} < 0^{\circ}$ | $0$: $\mbox{longitude} \geq 0^{\circ}$ | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $1|0|1$ | $6$ |
| $1$: $\mbox{latitude} < 0^{\circ}$ | $1$: $\mbox{longitude} < 0^{\circ}$ | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $1|1|0$ | $7$ |
| $1$: $\mbox{latitude} < 0^{\circ}$ | $1$: $\mbox{longitude} < 0^{\circ}$ | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $1|1|1$ | $8$ |
R, javascript, PHP, and Python language implementations to compute grid square codes are provided from here. In this library, we define the following functions:
- calculate the northern western geographic position of the grid (latitude, longitude) from meshcode
- meshcode_to_latlong_grid(meshcode)
- calculate the northern western geographic position of the grid (latitude, longitude) from meshcode
- meshcode_to_latlong_NW(meshcode)
- calculate the southern western geographic position of the grid (latitude, longitude) from meshcode
- meshcode_to_latlong_SW(meshcode)
- calculate the northern eastern geographic position of the grid (latitude, longitude) from meshcode
- meshcode_to_latlong_NE(meshcode)
- calculate the southern-eastern geographic position of the grid (latitude, longitude) from meshcode
- meshcode_to_latlong_SE(meshcode)
- calculate northern-western and southern-eastern geographic positions of the grid (latitude0, longitude0, latitude1, longitude1) from meshcode
- meshcode_to_latlong_grid(meshcode)
- calculate a basic (3rd level) grid square code (10 digits) from a geographical position (latitude, longitude)
- cal_meshcode(latitude,longitude)
- calculate a 1st level grid square code (6 digits) from a geographical position (latitude, longitude)
- cal_meshcode1(latitude,longitude)
- calculate a 2nd level grid square code (8 digits) from a geographical position (latitude, longitude)
- cal_meshcode2(latitude,longitude)
- calculate a 3rd level grid square code (10 digits) from a geographical position (latitude, longitude)
- cal_meshcode3(latitude,longitude)
- calculate a 4th level grid square code (11 digits) from a geographical position (latitude, longitude)
- cal_meshcode4(latitude,longitude)
- calculate a 5th level grid square code (12 digits) from a geographical position (latitude, longitude)
- cal_meshcode5(latitude,longitude)
- calculate a 6th level grid square code (13 digits) from a geographical position (latitude, longitude)
- cal_meshcode6(latitude,longitude)
The total number of 1st-level grid squares over the world is 360 $\times$ 180 $\times$ 3/2 = 97,200. The total number of 2nd-level grid squares is 64 times larger than the total number of 1stlevel grid squares. Thus, the total number of 2nd-level grid squares over the world is 6,220,800. The total number of 3rd-level grid squares is 100 times larger than the total number of 2nd-level grid squares and it is 622,080,000. The total number of 4th-level grid squares is 4 times larger than the total number of 3rd-level grid squares and it is 2,488,320,000. The total number of 5th-level grid squares is 4 times larger than the total number of 4th-level grid squares and it is 9,953,280,000. The total number of 6th-level grid squares is 4 times larger than 5th-level grid squares and it is 39,813,120,000.
Moreover, we can also approximate the total number of grid squares inland since Earth’s total landmass is 29.1998% of its total surface. Thus, the total number of each level grid squares over the world can be estimated as follows.
The total number of each level grid squares over the world.
| Layer type | # of grid squares | # of grid squares in land |
|---|---|---|
| 1st level | 97,200 | 28,383 |
| 2nd level | 6,220,800 | 1,816,461 |
| 3rd level | 622,080,000 | 181,646,116 |
| 4th level | 2,488,320,000 | 726,584,463 |
| 5th level | 9,953,280,000 | 2,906,337,853 |
| 6th level | 39,813,120,000 | 11,625,351,413 |
(c) 2015-2022 Research Institute for World Grid Squares