世界網格統計以及有關世界網格編碼之文檔
- 2017年2月27日,佐藤彰洋,椿廣計, “世界網格代碼的提案和世界網格統計的製作及有效利用“,第一屆計算社會科,學習院大學,東京都學研討會
- 2015年12月6日,佐藤彰洋,椿廣計, “網格統計的有效利用和向世界網格的擴展“, 第六屆橫幹連和學術會議,名古屋工業大學,名古屋市
- Aki-Hiro Sato, Shoki Nishimura, Hiroe Tsubaki, “World grid square codes: Definition and an example of world grid square data”, 2017 IEEE International Conference on Big Data (Big Data), pp. 4238–4247 (2017), DOI: 10.1109/BigData.2017.8258450
- Aki-Hiro Sato, Shoki Nishimura, Tsuyoshi Namiki, Naoki Makita, Hiroe Tsubaki, World Grid Square Data Reference Framework and its Potential Applications, Conference: 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), pp. 398-409 (2018), DOI: 10.1109/COMPSAC.2018.00062
網格統計的有效利用和向世界網格統計的擴展
1 簡介
地域網格編碼[1]在目前日本國內網格統計的計算上已經不可或缺了。日本總務省統計部透過E-Stat[2]從由地圖上看統計(統計GIS) [3]到國勢調查及政府實施的各種實態調查,都已經網格數據化並且對外開放了[4]。此外,國土交通省國土政策局情報課也將國土交通省所儲存的相 關位置的統計資料調查網格數據化並公開,甚至,地域網格的統計,對於災害時的受災範圍的試算、企業在推出新店鋪時的地區盈利試算以及公共政策的所需估計等方面都被廣泛地應用中。
像這樣的區域網格的統計數據在日本廣泛地被建立及利用,其背景,從地區網格統計制度的策定到被廣為利用,有著很長的歷史。
在本文中,我們將討論區域網格編碼,並概述筆者們在2015年9月號期刊所發表的《大數據時代所需要的標準化》[5]中所示的將區網格編碼擴張為世界網格編碼的方法。此外,我們也將討論當世界網格編碼成為全球標準規格時的應用之可能性。
2 地域網格編碼
在進入正題之前,讓我們先來概觀一下地區網格統計的歷史。地域網格統計是一種被稱為“網(grid)法”的統計方法。是一種将空間切割為某種區劃(grid或者mesh),利用單獨數據的區劃屬性,將它們的各個項目集中統計,製作出依存於空間統計數據的方法。
在計算地域網格統計時,首先需要对區劃進行定義。建立通用的區分方法,将使得不同組織為了不同目的所收集製作的地域網格統計數據之間,可以進行比較與結合。
本網格編碼(meshcode)於1973年7月12日由日本總理府統計局提出,之後在1976年1月以日本工業規格JIS X0410被設立為標準,如今在日本国内已經被廣泛的應用。
在地域網格統計中所使用的網格編碼,根據區域劃分的大小分為1級網格(80km*80km),2級網格(10km*10km),3級網格(1km*1km)(更小的劃分还有4級網格(500m*500m),5級網格(250m*250m),6級網格(125m*125m)
3級網格編碼呈現為一列8位數的數字,其前4位为1級網格編碼,前6位为2級網格編碼,從而對應到更大的網格。1級網格編碼下的1個區劃之緯度差是40分,經度差為1度。在日本附近一邊的長度約為80km。2級網格編碼下的1個區劃是將1級網格編碼的1個區劃在經度與緯度的方向各自分成了8等分後,緯度度差是5分,經度差為7分30秒,對應一邊長度約為10km的區域。3級網格編碼下的1個區劃是將2級網格編碼在經度與緯度的方向各自分成了10等分後,緯度差是30秒,經度差為45秒,對應一邊長度為1km的區域。
設$(\mbox{緯度},\mbox{經度})=(\mbox{latitude}, \mbox{longitude})$, 則表示由該經緯度所確定地點所屬的3級網格的地域網格編碼可由以下算式計算獲得。[1].
\begin{equation}
\mbox{grid square code} = pu qv rw.
\end{equation}
此處,整數值變量$p,u,q,v,r,w$的計算如下。
\begin{equation}
\left\{
\begin{array}{lcl}
\lfloor \mbox{latitude} \times 60 \div 40 \rfloor = p \quad (\mbox{$p$ is two digits.}),
%\label{eq:expression:p}
\\
a = (\mbox{latitude} \times 60 \div 40 – p) \times 40,
%\label{eq:expression:a}
\\
\lfloor a \div 5 \rfloor = q \quad (\mbox{$q$ is one digit.}),
%\label{eq:expression:q}
\\
b = (a \div 5 – q) \times 5,
%\label{eq:expression:b}
\\
\lfloor b \times 60 \div 30 \rfloor = r \quad (\mbox{$r$ is one digit.}),
%\label{eq:expression:r}
\\
c = (b \times 60 \div 30 – r) \times 30,
%\label{eq:expression:c}
\\
\lfloor \mbox{longitude} – 100 \rfloor = u \quad (\mbox{$u$ is two digits.}),
%\label{eq:expression:u}
\\
f = \mbox{longitude} – 100 – u,
%\label{eq:expression:f}
\\
\lfloor f \times 60 \div 7.5 \rfloor = v \quad (\mbox{$v$ is one digit.}),
%\label{eq:expression:v}
\\
g = (f \times 60 \div 7.5 – v) \times 7.5,
%\label{eq:expression:g}
\\
\lfloor g \times 60 \div 45 \rfloor = w \quad (\mbox{$w$ is one digit.}),
%\label{eq:expression:w}
\\
h = (g \times 60 \div 45 – w) \times 45,
%\label{eq:expression:h}
\end{array}
\right.
\end{equation}
同樣的反過来看, 從3級網格編碼$pu qv rw$也可以計算出該網格編碼西南角的緯度$\mbox{latitude}$與經度$\mbox{longitude}$。
\begin{equation}
\left\{
\begin{array}{lcl}
\mbox{latitude} &=& p \times 40 \ \div 60 + q \times 5 \div 60 + r \times 30 \div 3600, \\
\mbox{longitude} &=& 100 + u + v \times 7.5 \div 60 + w \times 45 \div 3600.
\end{array}
\right.
\end{equation}
透過網格編碼,可以得到將日本國土依照經度與緯度劃分為區域(網格)的唯一空間表現數列。然而,由於該網格編碼的定義僅限於日本國内的空間位置,在形式上,定異域範圍為東經100度到180度,北緯0度到66.66度(雖然在日本的鄰近國家與地區,如韓國、台灣等地,JIS X0410也可以直接使用。但是就筆者所知,在日本以外的鄰近地區並没有利用JIS X0410製作地域網格統計。)因此,網格編碼尚未覆蓋全球所有地方。在下一節中將討論把JIS X0410擴展到地球全體的方法。
3 JIS X041向世界網格編碼擴展
由於JIS X0410是以妥善劃分日本周邊地區為目的而設計的網格編碼,被網格定義的點$(\mbox{latitude},\mbox{longitude})$的定義域被限制為$0^{\circ} \leq \mbox{latitude} < 66.66^{\circ}$,
$100^{\circ} \leq \mbox{longitude} < 180^{\circ}$.
因此,僅僅依靠JIS X0410則難以表現日本以外地區的空間。為了克服這個問題,需要考慮如何將JIS X0410的網格編碼的計算方法擴展到$-90^{\circ} < \mbox{latitude} < 90^{\circ}$, $-180^{\circ} < \mbox{longitude} < 180^{\circ}$.
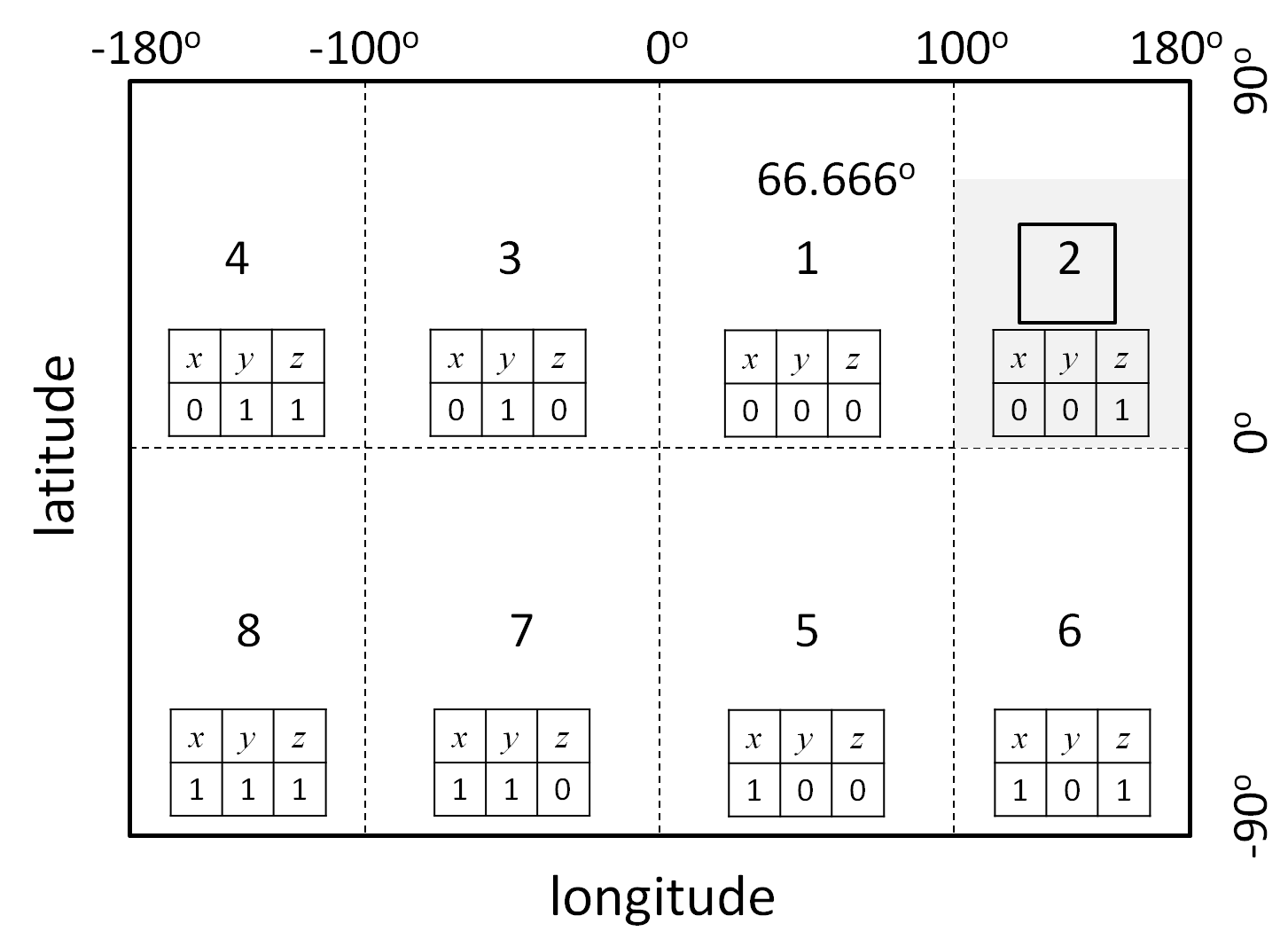
網格編碼的世界擴展及與0級網格編碼的關係.
如圖1所示, 全世界範圍内緯度與經度的定義域$-90 \leq \mbox{latitude} < 90^{\circ}$, $-180^{\circ} \leq \mbox{longitude} < 180^{\circ}$中,僅有陰影所示的部分為JIS X0410的網格編碼的定義域$0^{\circ} \leq \mbox{latitude} < 66.66^{\circ}$, $100^{\circ} \leq \mbox{longitude} < 180^{\circ}$.
在$0^{\circ} \leq \mbox{latitude} < 90^{\circ}$, $100^{\circ} \leq \mbox{longitude} < 180^{\circ}$中, $p$既可能是3位數也可能是1位數, $u$也可能是1位數. 因此, 首先, 關於1級網格編碼中對應緯度的$p$從2 digits擴展至3 digits. 如果$p$在10以下,則在前面添上00補成3 digits. 如果$p$在10以上100以下,则在前面添上0補成3 digits. 並且,$u$在10以下时也同樣在前面添上0補成2 digits. 接下来, 依照如下的條件来考慮將世界進行劃分。
1. 將緯度區分為南緯和北緯兩個狀態。因此,添加上表示北緯($x=0$)與南緯($x=1$)的1bit.
2. 將經度區分為東經和西經兩個狀態。因此, 添加上表示東經($y=0$)與西經($y=1$)的1bit.
3. 使用1bit來表示經度的絕對值在100$^{\circ}$以下和100$^{\circ}$以上兩個狀態,設$|\mbox{longitude}| \geq 100^{\circ}$($z=1$),$|\mbox{longitude}|<100^{\circ}$($z=0$).
包含現有的JIS X0410在内,一共有8個這樣的區域(参考圖1). 因此,將$xyz$3bit轉換為10進位之後全體加1,從而得到一個1位數(1到8)的数值作為擴展編碼。通過這個方法,理論上僅僅按照JIS X0410計算網格編碼,并且賦予一個1到8之間的1位數擴展編碼,就可以對擴展到世界範圍的網格編碼進行定義。表1總結了1到8的擴展編碼所對應的地球上的領域。像這樣定義的從1到8的1位數擴張編碼為了方便被稱為0級網格編碼。
已知$xyz$的時候, 0級網格編碼$o$的計算方法是,
\begin{equation}
o=2^2 x + 2 y + z + 1.
\end{equation}
. 另外,當已知0級網格編碼$o$(1~8)的時候,$xyz$可由如下計算獲得。
\begin{eqnarray}
z &=& (o – 1) \mbox{ mod } 2, \\
y &=& ((o – z – 1) \div 2) \mbox{ mod } 2, \\
x &=& (o – 2 \times y – z – 1) \div 4,
\end{eqnarray}
當已知由緯度$\mbox{latitude}$和經度$\mbox{longitude}$表示的位置信息(WGS84)的時候,各級網格編碼的整數值的計算公式可以擴展如下。
1級網格編碼
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0u & (p < 10, u < 10) \\
o0p0u & (10 \leq p < 100, u < 10) \\
op0u & (p \geq 100, u < 10) \\
o00pu & (p < 10, u \geq 10) \\
o0pu & (10 \leq p < 100, u \geq 10) \\
opu & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
2級網格編碼
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqv & (p < 10, u < 10) \\
o0p0uqv & (10 \leq p < 100, u < 10) \\
op0uqv & (p \geq 100, u < 10) \\
o00puqv & (p < 10, u \geq 10) \\
o0puqv & (10 \leq p < 100, u \geq 10) \\
opuqv & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
3級網格編碼
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrw & (p < 10, u < 10) \\
o0p0uqvrw & (10 \leq p < 100, u < 10) \\
op0uqvrw & (p \geq 100, u < 10) \\
o00puqvrw & (p < 10, u \geq 10) \\
o0puqvrw & (10 \leq p < 100, u \geq 10) \\
opuqvrw & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
4級網格編碼
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2 & (p < 10, u < 10) \\
o0p0uqvrws_2 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2 & (p \geq 100, u < 10) \\
o00puqvrws_2 & (p < 10, u \geq 10) \\
o0puqvrws_2 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
5級網格編碼
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
6級網格編碼
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4s_8 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4s_8 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4s_8 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4s_8 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4s_8 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4s_8 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}
其中,各整數值可由如下計算獲得。
\begin{equation}
\left\{
\begin{array}{l}
p: = \lfloor (1-2x)\mbox{latitude} \times 60 \div 40 \rfloor \quad (\mbox{$p$ is two or three digits}),
\\
a := \bigl\{(1-2x)\mbox{latitude} \times 60 \div 40 – p\bigr\} \times 40, \\
q := \lfloor a \div 5 \rfloor \quad (\mbox{$q$ is one digit}),
\\
b := (a \div 5 – q) \times 5,
\\
r := \lfloor b \times 60 \div 30 \rfloor \quad (\mbox{$r$ is one digit}),
\\
c := (b \times 60 \div 30 – r) \times 30,
\\
s_{2u} := \lfloor c/15 \rfloor \quad (\mbox{$s_{2u}$ is one digit}),
\\
d := (c/15-s_{2u}) \times 15,
\\
s_{4u} := \lfloor d/7.5 \rfloor \quad (\mbox{$s_{4u}$ is one digit}),
\\
e := (d/7.5-s_{4u}) \times 7.5,
\\
s_{8u} := \lfloor e/3.75 \rfloor \quad (\mbox{$s_{8u}$ is one digit}),
\\
u := \lfloor (1-2y)\mbox{longitude} – 100z \rfloor \quad (\mbox{$u$ is one or two digits}),
\\
f := (1-2y)\mbox{longitude} – 100z – u,
\\
v := \lfloor f \times 60 \div 7.5 \rfloor \quad (\mbox{$v$ is one digit}),
\\
g := (f \times 60 \div 7.5 – v) \times 7.5,
\\
w := \lfloor g \times 60 \div 45 \rfloor \quad (\mbox{$w$ is one digit}),
\\
h := (g \times 60 \div 45 – w) \times 45,
\\
s_{2l} := \lfloor h/22.5 \rfloor \quad (\mbox{$s_{2l}$ is one digit}),
\\
i := (h/22.5-s_{2l}) \times 22.5,
\\
s_{4l} := \lfloor i/11.25 \rfloor \quad (\mbox{$s_{4l}$ is one digit}),
\\
j := (i/11.25-s_{4l}) \times 11.25,
\\
s_{8l} := \lfloor j/5.625 \rfloor \quad (\mbox{$s_{8l}$ is one digit}),
\\
s_2 := s_{2u} \times 2+s_{2l}+1 \quad (\mbox{$s_{2}$ is one digit}),
\\
s_4 := s_{4u} \times 2+s_{4l}+1 \quad (\mbox{$s_{4}$ is one digit}),
\\
s_8 := s_{8u} \times 2+s_{8l}+1 \quad (\mbox{$s_{8}$ is one digit})
\end{array}
\right..
\end{equation}
反過来,已知1級網格編碼 $opu$ ($o$(1 digit), $p$(3 digits), $u$(2 digits))的時候,表示其西北角位置的緯度$\mbox{latitude}$和經度$\mbox{longitude}$可由
\begin{eqnarray}
\mbox{latitude} &=& (1-2x) \bigl\{(p-x+1) \times 40 \ \div 60 \bigr\}, \\
\mbox{longitude} &=& (1-2y) (100 \times z + u+y ).
\end{eqnarray}
計算得出。
已知2級網格編碼 $opuqv$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit))的時候,表示其西北角位置的緯度$\mbox{latitude}$和經度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl\{p \times 40 \ \div 60 \\
&+& (q-x+1) \times 5 \div 60 \bigr\}, \\
\label{eq:expression2:latitude-mesh-2}
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u \\
\nonumber
&+& (v+y) \times 7.5 \div 60 \bigr).
\label{eq:expression2:longitude-mesh-2}
\end{eqnarray}
計算得出。
已知3級網格編碼 $opuqvrw$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit)) 的時候,表示其西北角位置的緯度$\mbox{latitude}$和經度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
&+& (r-x+1) \times 30 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-3}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
&+& (w+y) \times 45 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-3}
\end{eqnarray}
計算得出。
已知4級網格編碼 $opuqvrws_2$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1digit)) 的時候,表示其西北角位置的緯度$\mbox{latitude}$和經度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
&+& \lfloor (s_2-1)/2 \rfloor + x-1) \times 15 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-4}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-4}
\end{eqnarray}
計算得出。
已知5級網格編碼 $opuqvrws_2s_4$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), $s_4$(1 digit))的時候,表示其西北角位置的緯度$\mbox{latitude}$和經度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& \lfloor (s_2-1)/2 \rfloor + x-1)) \times 15 \div 3600 \\
&+& \lfloor (s_4-1)/2 \rfloor + x-1)) \times 7.5 \div 3600\bigr), \\
\label{eq:expression2:latitude-mesh-5}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-5}
\end{eqnarray}
計算得出。
已知6級網格編碼 $opuqvrws_2s_4s_8$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), $s_4$(1 digit), $s_8$(1 digit)) 的時候,表示其西北角位置的緯度$\mbox{latitude}$和經度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& \lfloor (s_2-1)/2 \rfloor + x-1)) \times 15 \div 3600 \\
\nonumber
&+& \lfloor (s_4-1)/2 \rfloor + x-1)) \times 7.5 \div 3600 \\
&+& \lfloor (s_8-1)/2 \rfloor + x-1)) \times 3.75 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-6}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
\nonumber
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \\
&+& (((s_8-1) \mbox{ mod } 2) – y) \times 5.625 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-6}
\end{eqnarray}
計算得出。
將JIS X0410擴展到世界範圍的擴展編碼(0級網格編碼)的定義.
| $x$: 緯度 | $y$: 經度 | $z$: 經度的範圍 | $x|y|z$ | 10進位制表示 |
|---|---|---|---|---|
| $0$: 北緯 ($\mbox{latitude} > 0^{\circ}$) | $0$: 東經 ($\mbox{longitude} > 0^{\circ}$) | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $0|0|0$ | $1$ |
| $0$: 北緯 ($\mbox{latitude} > 0^{\circ}$) | $0$: 東經 ($\mbox{longitude} > 0^{\circ}$) | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $0|0|1$ | $2$ |
| $0$: 北緯 ($\mbox{latitude} > 0^{\circ}$) | $1$: 西經 ($\mbox{longitude} < 0^{\circ}$) | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $0|1|0$ | $3$ |
| $0$: 北緯 ($\mbox{latitude} > 0^{\circ}$) | $1$: 西經 ($\mbox{longitude} < 0^{\circ}$) | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $0|1|1$ | $4$ |
| $1$: 南緯 ($\mbox{latitude} < 0^{\circ}$) | $0$: 東經 ($\mbox{longitude} > 0^{\circ}$) | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $1|0|0$ | $5$ |
| $1$: 南緯 ($\mbox{latitude} < 0^{\circ}$) | $0$: 東經 ($\mbox{longitude} > 0^{\circ}$) | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $1|0|1$ | $6$ |
| $1$: 南緯 ($\mbox{latitude} < 0^{\circ}$) | $1$: 西經 ($\mbox{longitude} < 0^{\circ}$) | $0$: $|\mbox{longitude}| < 100^{\circ}$ | $1|1|0$ | $7$ |
| $1$: 南緯 ($\mbox{latitude} < 0^{\circ}$) | $1$: 西經 ($\mbox{longitude} < 0^{\circ}$) | $1$: $|\mbox{longitude}| \geq 100^{\circ}$ | $1|1|1$ | $8$ |
像這樣定義之後,在迄今依照JIS X0410定義的網格編碼前添加上0級網格編碼2和1級網格編碼0之後即可擴展為世界網格編碼。
在這裡所介绍的筆者們提出的世界網格編碼的試行,以R语言安裝並公開中[10]。在資料庫中定義了以下的函数。
-
- 輸出世界3級網格四角的緯度和
- meshcode_to_latlong_grid(meshcode)
-
- 輸出世界3級網格西北角的緯度和經度
- meshcode_to_latlong_NW(meshcode)
-
- 輸出世界3級網格西南角的緯度和經度
- meshcode_to_latlong_SW(meshcode)
-
- 輸出世界3級網格東北角的緯度和經度
- meshcode_to_latlong_NE(meshcode)
-
- 输出世界3級網格東南角的緯度和經度
- meshcode_to_latlong_SE(meshcode)
-
- 輸出位置信息(緯度和經度)以及包含該位置的世界3級網格編碼
- cal_meshcode(latitude,longitude)
地球是半径$r$大約為6,371km的球體,其表面積$S$大約為$S = 510,100,000$ km$^2$. 覆蓋全球的1級網格的總數為 360 $\times$ 180 $\times$ 3/2 = 97,200. 2級網格的總數為1級網格的64倍,因此覆蓋全球的2級網格的总總數 6,220,800. 3級網格的總數為2級網格的100倍,因此覆蓋全球的3級網格的總數為 622,080,000. 4級網格的總數是3級網格的4倍,因此4級網格的總數為2,488,320,000. 5級網格的總數更是為4級網格的4倍,因此5級網格的總數為9,953,280,000. 6級網格的總數是5級網格的4倍,因此6級網格的總數為39,813,120,000.
另外,地球上陸地面積約占全球的29.2998%,各級世界網格的總數以及陸地上世界網格的總數分别總結如下表。
覆蓋全球的世界網格的總數和陸地上世界網格的總數.
| 世界網格級别 | 覆蓋全球的網格總數 | 陸地上網格總數 |
|---|---|---|
| 1級網格 | 97,200 | 28,383 |
| 2級網格 | 6,220,800 | 2,838,220 |
| 3級網格 | 622,080,000 | 181,646,116 |
| 4級網格 | 2,488,320,000 | 726,584,463 |
| 5級網格 | 9,953,280,000 | 2,906,337,853 |
| 6級網格 | 39,813,120,000 | 11,625,351,413 |
- [1] 總務省統計局 地域網格統計的概要 [10 August 2015] http://www.stat.go.jp/data/mesh/gaiyou.htm
- [2] e-Stat https://www.e-stat.go.jp/SG1/estat/eStatTopPortal.do
- [3] 從地圖上看統計(統計GIS)https://www.e-stat.go.jp/SG1/estat/toukeiChiri.do?method=init
- [4] 國土交通省國土政策局國土情報課 http://www.mlit.go.jp/kokudoseisaku/kokudojoho.html
- [5] 佐藤彰洋, 椿廣計, 大數據時代必須的標準化, 統計, 2015年9月号, pp.32–38.
- [6] 有關国土實態總合統計之開発・整備之研究報告(昭和46年)發行:總理府統計局
- [7] 國土交通省観光廳 http://www.mlit.go.jp/kankocho/
- [8] 住宿旅行統計調査 http://www.mlit.go.jp/kankocho/siryou/toukei/shukuhakutoukei.html
- [9] 利用世界網格編碼的R言語的計算用資料庫在以下的URL公開中. https://www.fttsus.jp/worldmesh/library.html
- [10] Ordnance Survey National Grid reference system http://www.ordnancesurvey.co.uk/support/the-national-grid.html
- [11] Ordnance Survey http://www.ordnancesurvey.co.uk/support/understanding-gis/standards.html
- [12] EUR Report 21494 EN:39-46 http://www.ec-gis.org/sdi/publist/pdfs/annoni2005eurgrids.pdf
- [13] GEOSTAT_Grid_POP_2006_1K http://www.efgs.info/data/geostat/open-data
- [14] Amante, C. and B.W. Eakins, 2009. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. NOAA Technical Memorandum NESDIS NGDC-24. National Geophysical Data Center, NOAA. doi:10.7289/V5C8276M Accessed on 13 May 2013.